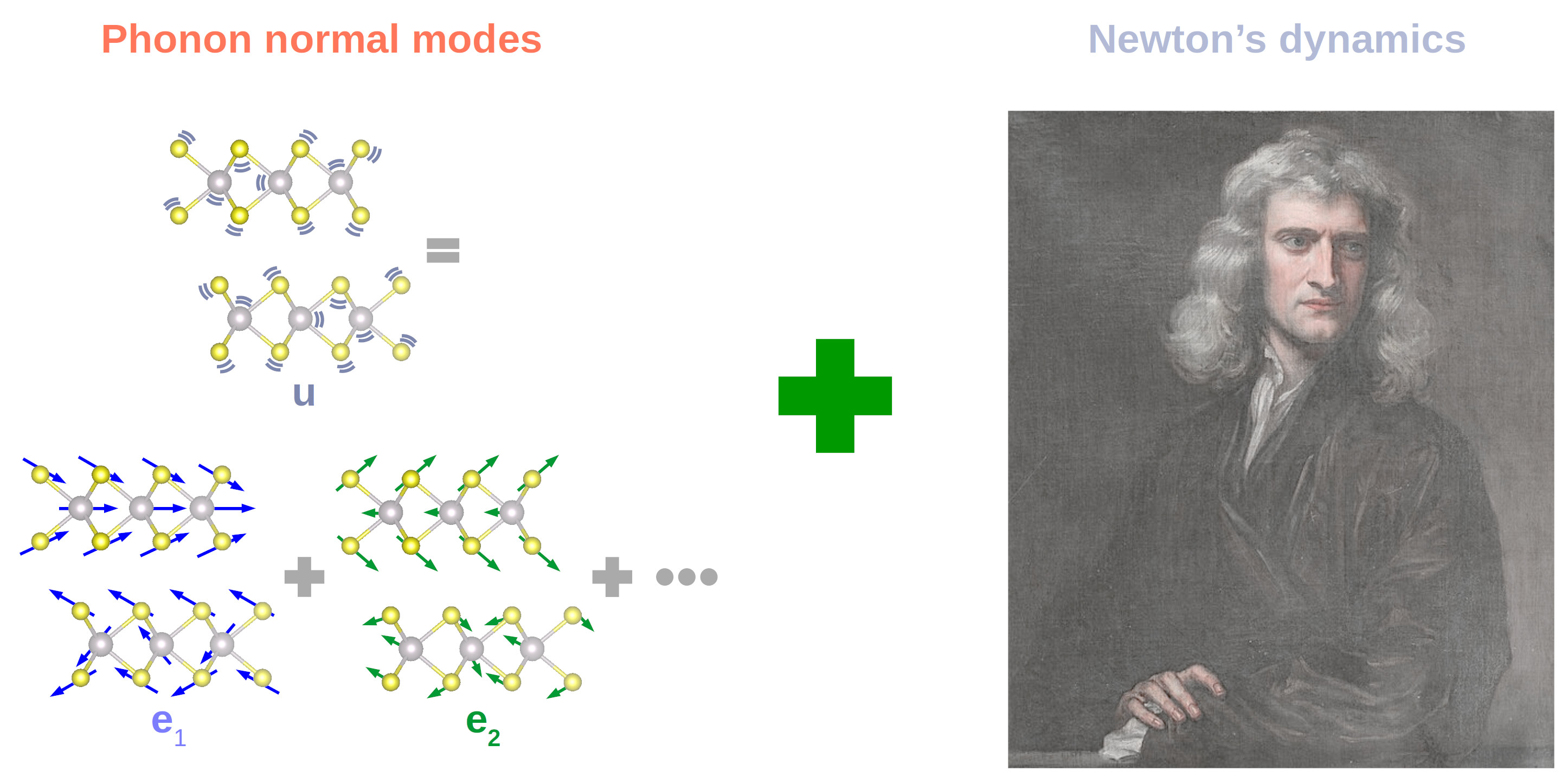
What is it about?
Normal Dynamics is a new technique to solve Newton's equations which can obtain an easy computational speedup by a fine tune of the Brillouin zone sampling and can account for distortions realized across large atomic distances without the use of large simulation cells. The technique is general and can be used to simulate periodic, semiperiodic, and finite systems such as crystals, slabs, nanoclusters, or molecules. The technique is implemented in the open source PINDOL available free of charge in the github repository https://github.com/acammarat/pindol
Featured Image
Why is it important?
Normal Dynamics exploits the Taylor expansion of the potential energy which is a straightforward parameterisation of atomic interactions; this avoid the user the burden to look for specific force fields. The integration of the equations of motion in the reciprocal space allows to account for distortions realized across large atomic distances without the use of large simulation cells.
Perspectives

The normal dynamics scheme provides a straightforward decomposition of the atomic motions in terms of normal coordinates, thus facilitating the analysis of several phenomena such as heat transfer, hydrodynamic phonon transport, carrier transport, thermoelectric effect, and energy dissipation in tribological conditions. The normal equations of motion can be modified in order to include atomic constraints or the presence of external forces that may simulate, for example, an external field exciting specific phonon modes or dragging forces producing atomic drifts. The Normal Dynamics technique and the PINDOL software can be interfaced with structure databases and used in high-throughput calculations for the discovery of new materials with target physical properties.
Dr. Antonio Cammarata
Ceske Vysoke Uceni Technicke v Praze
Read the Original
This page is a summary of: Integrating Newton’s equations of motion in the reciprocal space, The Journal of Chemical Physics, August 2024, American Institute of Physics,
DOI: 10.1063/5.0224108.
You can read the full text:
Contributors
The following have contributed to this page