What is it about?
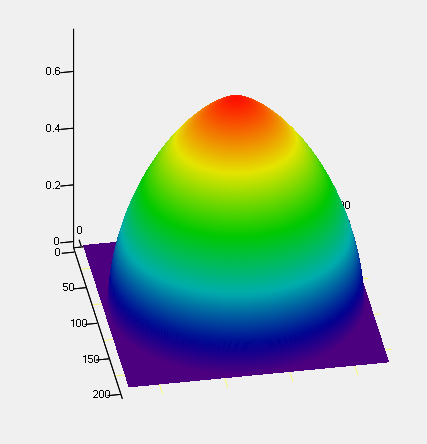
To the qualitative properties of self-similar solutions of a cross-diffusion parabolic system not in divergence form with a source Abstract. The property of a finite speed of a perturbation distribution for the Cauchy problem for the non-divergence form of the parabolic equation based on the comparison method and the asymptotic behavior of a self-similar solution are achieved. The resulting asymptotics have been used as an initial approximation, and numerical solutions have been calculated.
Featured Image

Photo by Joël de Vriend on Unsplash
Why is it important?
The aim of this paper is to study of influence a variable density to an evaluation of the nonlinear processes. It is proved Fujita type global solvability, asymptotic properties of the self-similar solution based on an algorithm of nonlinear splitting. It is solved the problem with an initial approximation for the numerical solution of Cauchy problem, it is suggested the numerical scheme method and algorithm of solution keep nonlinear properties solution of fast diffusion and slow diffusion cases.
Perspectives

You can use this equation for image restoration, that is proved by the method comparison.
Mr. Makhmud Bobokandov
National University of Uzbekistan
Read the Original
This page is a summary of: Cauchy problem for the heat dissipation equation in non-homogeneous medium, January 2023, American Institute of Physics,
DOI: 10.1063/5.0144807.
You can read the full text:
Resources
Contributors
The following have contributed to this page