What is it about?
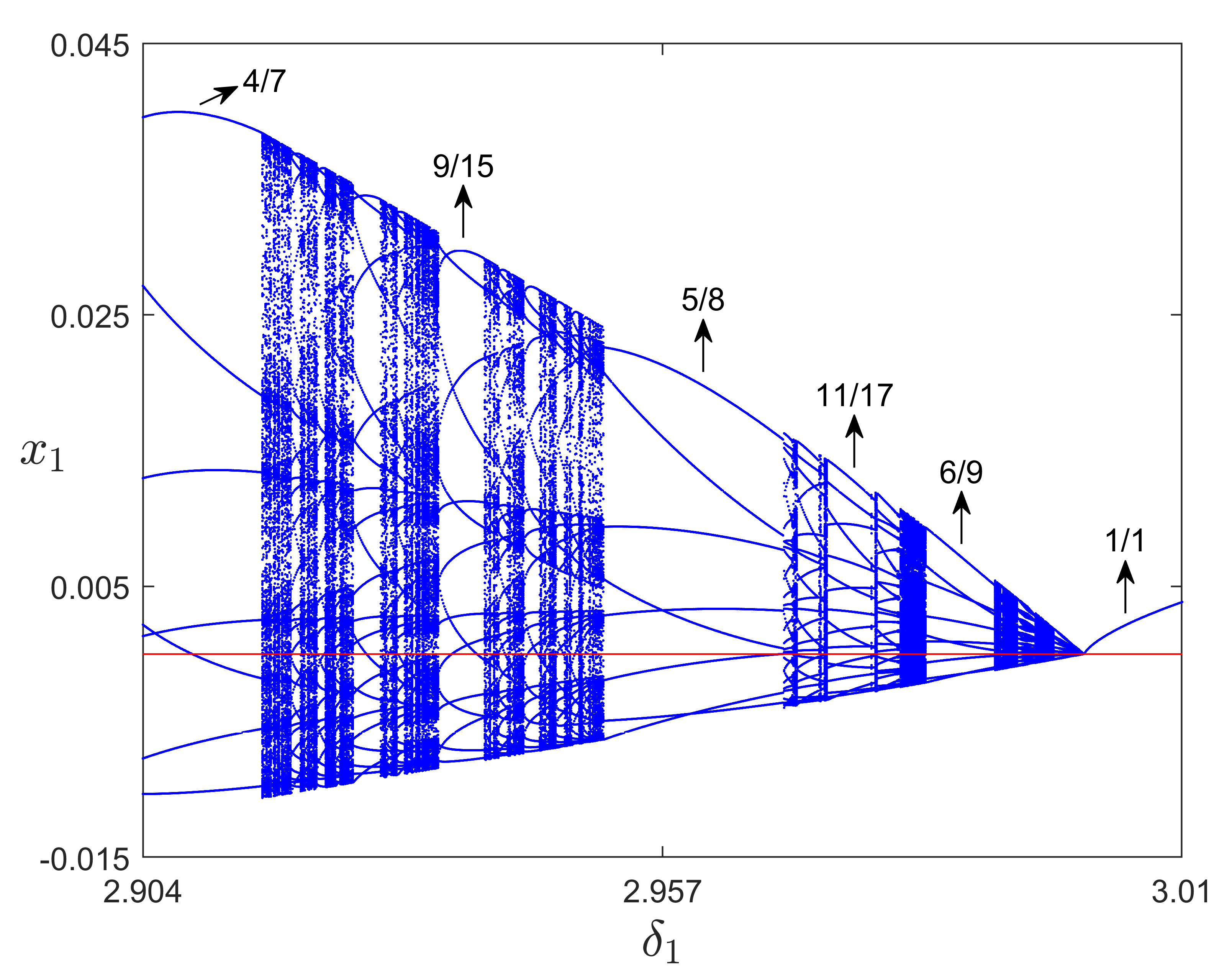
In this paper we investigate the grazing-sliding bifurcations in a dry-friction oscillator. We first obtain conditions of the existence of grazing-sliding orbits numerically by using the shooting method. Then we compute the lower and the higher order approximations of the Poincare map respectively by the method of zero-time discontinuity mapping. We find that there are big differences between the lower order map and the original system and the higher order map can effectively reduce such disagreements. By using the higher order map and numerical simulations, we find that the system undergoes very complicated dynamical behaviors near the grazing-sliding bifurcation point, such as period-adding cascades and chaos.
Featured Image

Photo by Ricardo Gomez Angel on Unsplash
Why is it important?
As far as we know, this is the first work on higher order computations of the discontinuity mapping for sliding bifurcations, and the phenomena of period-adding cascades arising from sliding bifurcations have not been reported previously. We believe that our methods can be also applied to study crossing-sliding, switching-sliding and adding-sliding bifurcations.
Perspectives

Our results show that the near grazing-sliding dynamics of dry-friction systems are very rich. There are many problems to be solved. For example, in reality, many systems are excited by more than one frequency. Consequently, it is very important to study sliding bifurcations for piecewise smooth systems under nonharmonic or quasi-periodic excitations, which is much more difficult. We plan to focus on those issues in our future work. I also would like to take this opportunity to thank my co-author for the collaborations.
Zhengdong Du
Sichuan University
Read the Original
This page is a summary of: Grazing–sliding bifurcation in a dry-friction oscillator on a moving belt under periodic excitation, Chaos An Interdisciplinary Journal of Nonlinear Science, October 2024, American Institute of Physics,
DOI: 10.1063/5.0233501.
You can read the full text:
Contributors
The following have contributed to this page